Blood is technically a specialized connective tissue. It is made up of blood cells and plasma.
Plasma is the stuff we think about that’s mostly fluid: lots of water, ions (charged particles), nutrients from food, waste products, oxygen, carbon dioxide, hormones, vitamins, and then we have 3 really specific types of proteins and these are really chunky proteins.
Albumin doesn’t seem important at first, cause all it does is prevent water from leaving the capillaries but if you think about it, if all the liquid diffuses too fast out of your capillaries, that would be disastrous. So you want albumin floating around to hold some of that water in.
Globulins are antibodies that transport other things.
Fibrinogen are specifically for blood clotting.
Total blood volume for males: 5-6 liters. For females: 4-5 liters.
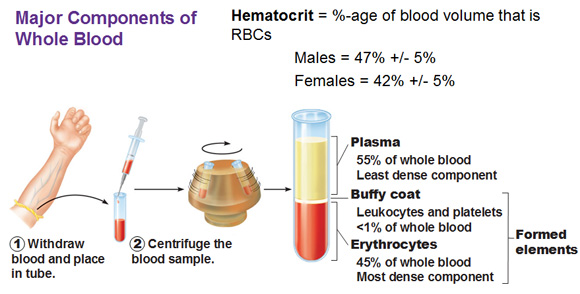
Above: In this picture we take some blood and put it in a test tube and put it slanted on a centrifuge so that the heavy stuff is pushed to the bottom. The bottom stuff are erythrocytes (From Ancient Greek, eruthrós = red). Then we have a little thin layer called buffy coat and then this whole big top part is plasma which is all that fluid and all the things that are dissolved in that fluid.
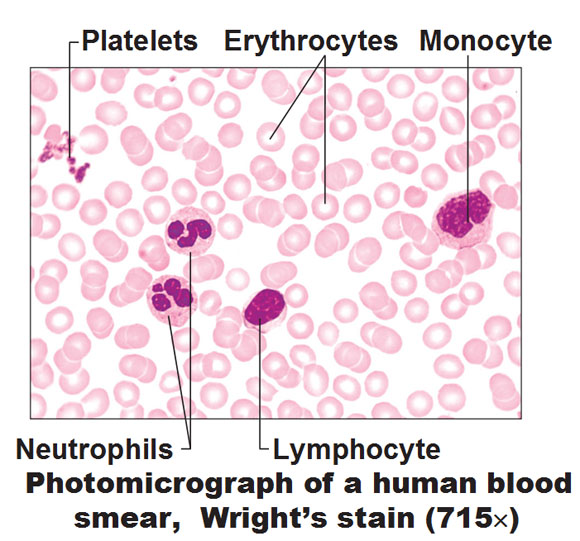
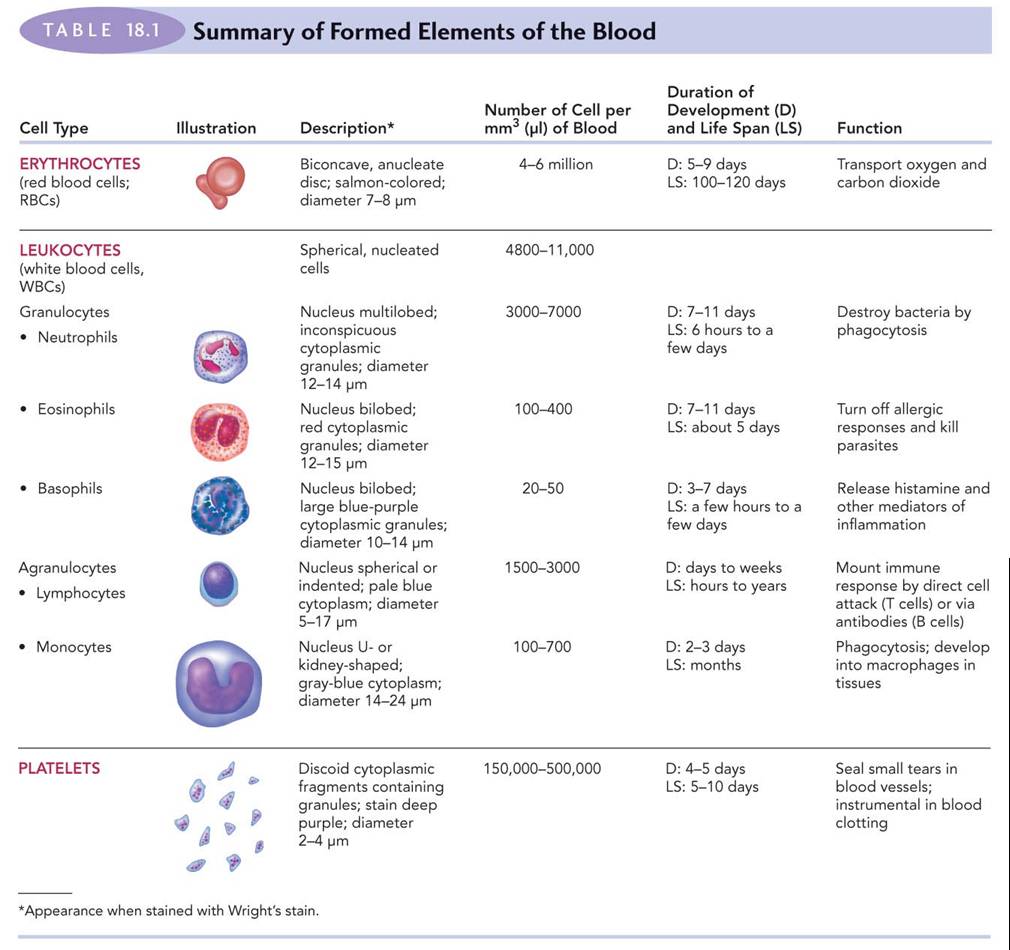
Above: If you take some blood from a finger and put it on a slide, this is what you’d see. This is a smear. Most of these cells are red blood cells or erythrocytes (pink with white centers; anucleated). Platelets are little pieces broken off from big cells that are used later for the blood clotting process. The neutrophils, lymphocytes and monocytes are a different kind of blood cell called leukocytes and the graphic below gives us an overall summary of the different types of blood cells.
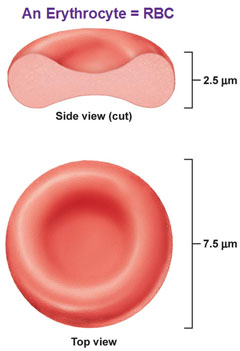
Let’s look at erythrocytes
Look at this bi concave shape, what is so important or great about this shape? Floating? Nah. Flexible? It’s a very flexible cell so in case it needs to go through a capillary or a bend it can. But there’s something else… If you take a sphere and flatten and add a concave surface to each side, suddenly you’ve increased the surface area. So why is that good? For taking oxygen in (or letting co2 out) and you’ve also brought the edges closer together so gas doesn’t have to move as far. You want the gas exchange to be quick, on the microscopic level so you’re always ready. We’re going to put some hemoglobin in there that’s going to hold the oxygen molecules thanks to its affinity to iron atoms. A mature RBC has no organelles, including no nucleus and no mitochondria. The nucleus just takes too much space. We want as much space to pack in as much oxygen as much as possible. If you have a big chunky nucleus in there, you’ve wiped out like half your oxygen. But it’s not there, so you have lots of space. We also have no mitochondria because once its mature, it’s solely engineered for one purpose, to carry oxygen (and co2). It doesn’t need to produce any protein because it’s going to die off in 120 days anyway. So we don’t need any proteins to repair this or repair that, we don’t need any of that stuff. It doesn’t use any of the oxygen its carrying either because it survives anaerobically through glucose broken down in your body.
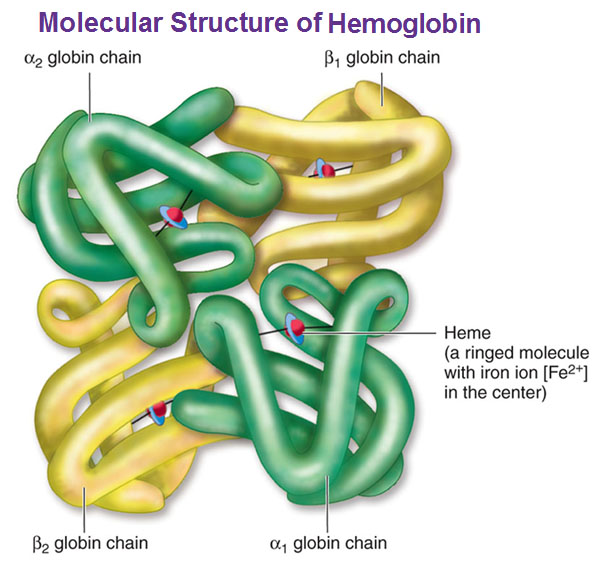
Hemoglobin
We have four protein chains, each protein chain is galled a globin. Two of them are beta and two are alpha. You could see below these chains are contorted into these shapes. A heme is a ringed shape molecule with an iron ion (fe +2) and oxygen happens to be attracted to a charged ion. For each hemoglobin molecule we have four hemes, so we have space for four oxygen molecules to be carried and we have 280 million hemoglobin molecules for every erythrocyte. So a single red blood cell can carry 1 billion oxygen molecules (280 million times 4). So that’s your hemoglobin deal.
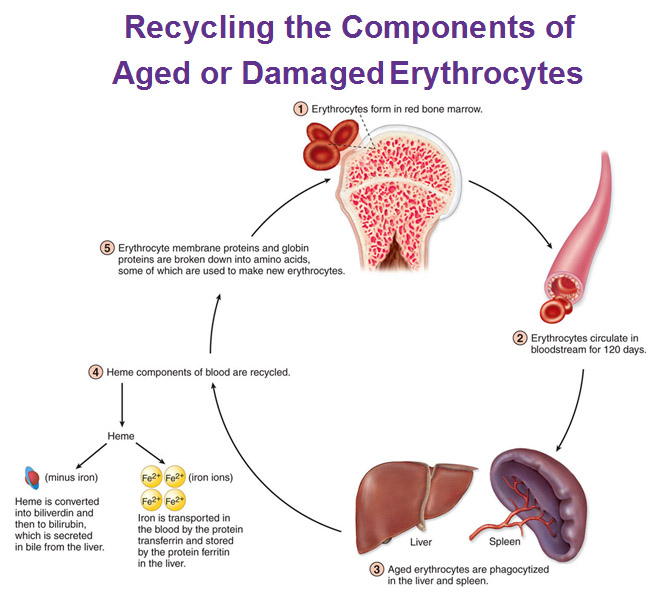
Recycling Erythrocytes
Blood cells recirculate every 120 days and the liver and the spleen are in charge of sequestering those worn out erythrocytes. They collect them, phagocytize them (eat them), break them down, take the cell membrane stuff and break those down into amino acids. But lets look at the hemes specifically. The hemes are split apart and those iron ions are stored in the liver. The ring part (without the iron) is broken down into billiverdin and that’s going to be secreted in the bile from the liver. This iron that is stored in the liver meanwhile can certainly be recycled so we’re going to make a whole new batch of RBC’s. That’s why liver is a good thing to eat to build up some RBC, if you could stand it.
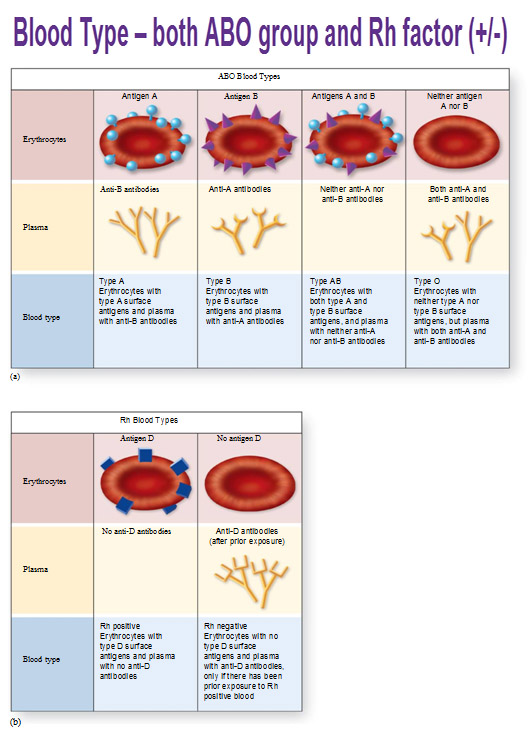
Blood Type
Blood types have a structural basis for them. The blood type is determined by certain proteins that are embedded in the cell membrane of your RBC’s and they are sticking out. This is where that idea becomes very important. The proteins are like markers that determine what blood type you have.
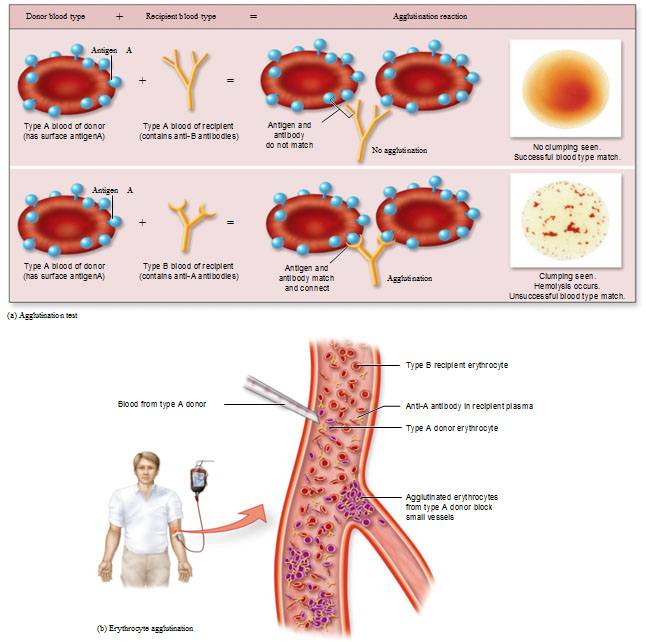
Using an example in the picture below, we have these proteins sticking out represented by blue, spherical shapes. This one is called Antigen A, and you’re going to be type A blood if you have this. Another person has an antigen shape that is different that looks like triangles and that’s Antigen B. Next is a person that has both shapes of A’s and B’s so that person is Type AB. This last person with neither antigens are called Type O. This is all determined by your genes that are programmed to produce proteins that are shaped in a particular way.
Let’s say you’re a Type A blood person. You’re going to produce antibodies to protect yourself against the B antigens. You see the shape of the antibodies that have the shape of the alternative antigen? Anti-B antibodies match spherical shape of the antigen A and vice versa. If you’re an O person, you produce one of each, some of the A antibodies and some of the B antibodies.
Rh Factor and RhoGAM injection
Another type of protein that is exposed on RBC, a different sort of family, is called a Rh factor. You either have it or you don’t. Above they show it as a square to have it as a different shape. The person who has the antigen D is positive and one who doesn’t, is negative. So someone could be Type A and Rh positive or negative for example.
Rh factor is really only important in a pregnant woman. Let’s say a woman is Rh negative and the father of the baby gave the baby the genes to have a positive Rh factor. It’s okay because the babies blood isn’t mixing with the mothers or vice-versa. When it becomes important is when she gives birth to the baby because there’s a break in the blood systems and everything sort of tears a little bit and some of the blood cells from the baby could cross over into the mothers system at that moment of birth and if that sort of goes with no acknowledgement or treatment, the mothers system will recognize that and produce a bunch of these square antibodies to get rid of those. The Rh- negative mother will produce Rh antibodies upon exposure to Rh factor. These antibodies are going to be floating in the blood and if, on the next baby, the baby is Rh positive, the mothers system can cross over to the babies system and attack the baby. This wasn’t figured out until the early 1900’s and took even longer to figure out what to do about that. Those subsequent babies that were Rh Positive, if they even survived, lived a very short lifespan. This injection was created called RhoGAM that is given to the mother for the first child of the baby in the 2nd half of pregnancy and within 72 hours of birth to kill the Rh+ cells that have crossed into her blood stream to prevent her from making Rh antibodies. This way when she has her second baby it’s like starting fresh.
Agglutination Reaction aka clumping test
Our last thing is Agglutination. If you give the wrong blood type to somebody, they’re going to attack that blood and create clumps and problems. So we’re going to do this test in a test tube to see if there’s clumping or not. This is how you figure out what someones blood type is. Blood O can be given to anybody because there’s nothing on the blood cells for the person to attack. So Blood O person would be a “Universal donor” because it won’t cause any conflict with any recipients antibodies. The flipside of that would be somebody who is type AB. They carry both AB antigens, but no antibodies, so they can receive anyone’s blood because they don’t have antibodies to fight antigens. Type AB is known as a “Universal recipient.”
Use this Table of Contents to go to the next article

YOU ARE HERE AT THE CARDIOVASCULAR SYSTEM